Advertisements
Advertisements
Question
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
Solution
Given that, if perpendicular from any point within, an angle on its arms is congruent, prove that it lies on the bisector of that angle
Now,
Let us consider an angle ABC and let BP be one of the arm within the angle
Draw perpendicular PN and PM on the arms BC and BA such that they meet BC and BA in N and M respectively.
Now, in ΔBPM and ΔBPN
We have ∠BMP= BNP = 90° [given]
BP=BP [Common side]
And MP=NP [given]
So, by RHS congruence criterion, we have
ΔBPM≅ΔBPN
Now,
∠MBP=∠NBP [ Corresponding parts of congruent triangles are equal]
⇒ BP is the angular bisector of ∠ABC
∴ Hence proved

APPEARS IN
RELATED QUESTIONS
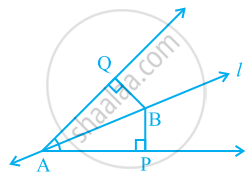
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
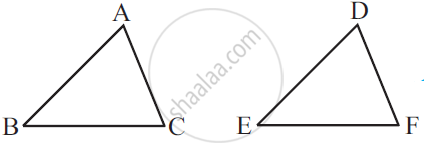
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
Use the information in the given figure to prove:
- AB = FE
- BD = CF

From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
