Advertisements
Advertisements
प्रश्न
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
उत्तर
Given that, if perpendicular from any point within, an angle on its arms is congruent, prove that it lies on the bisector of that angle
Now,
Let us consider an angle ABC and let BP be one of the arm within the angle
Draw perpendicular PN and PM on the arms BC and BA such that they meet BC and BA in N and M respectively.
Now, in ΔBPM and ΔBPN
We have ∠BMP= BNP = 90° [given]
BP=BP [Common side]
And MP=NP [given]
So, by RHS congruence criterion, we have
ΔBPM≅ΔBPN
Now,
∠MBP=∠NBP [ Corresponding parts of congruent triangles are equal]
⇒ BP is the angular bisector of ∠ABC
∴ Hence proved

APPEARS IN
संबंधित प्रश्न
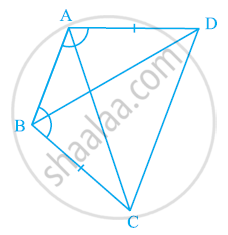
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
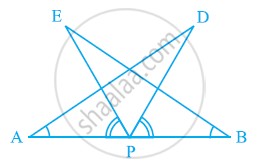
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
In the given figure, AB = DB and Ac = DC.
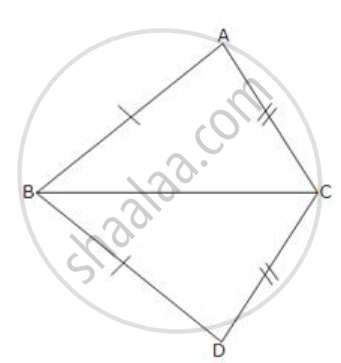
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
