Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
उत्तर
ABCD is a parallelogram, The sides AB and AD are produced to E and F respectively,
such that AB = BE and AD = DF
We need to prove that ΔBEC ≅ ΔDCF.

Proof:
AB = DC ...[ Opposite sides of a parallelogram ] ...(1)
AB = BE ...[ Given ] ...(2)
From (1) and (2), We have
BE = DC ...(3)
AD = BC ...[ Opposite sides of a parallelogram ] ...(4)
AD = DF ....[Given] ...(5)
From (4) and (5), we have
BC = DF ...(6)
Since AD II BC, the corresponding angles are equal.
∴ ∠DAB = ∠CBE ...(7)
Since AB II DC, the corresponding angles are equal.
∴ ∠DAB = ∠FDC ...(8)
From (7) and (8), we have
∠CBE = ∠FDC
ln ΔBEC and ΔDCF
BF = DC ....[ from (3) ]
∠CBE = ∠FDC ...[ from (9) ]
BC = DF ....[ from (6) ]
∴ By Side-Angle-Side criterion of congruence,
ΔBEC ≅ ΔDCF
Hence proved.
APPEARS IN
संबंधित प्रश्न
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

In the given figure, prove that:
CD + DA + AB + BC > 2AC

In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
In the given figure, AB = DB and Ac = DC.
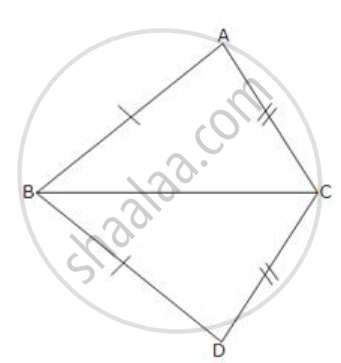
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
