Advertisements
Advertisements
प्रश्न
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
उत्तर
The given information and corresponding figure is given below
AB = AD
BC = CD

From the figure, we have
AB = AD (given)
CB = CD (given)
And,
AC = AC (common sides)
Hence, triangles ABC and ADC are congruent to each other.
APPEARS IN
संबंधित प्रश्न
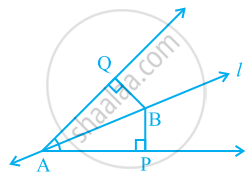
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

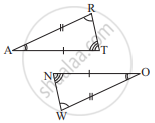
In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ΔRAT ≅ ?
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
