Advertisements
Advertisements
प्रश्न
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
उत्तर
We have given, ΔABC which is an isosceles right triangle with AB = AC and AD is the bisector of ∠A.
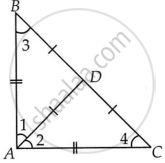
Now in ΔABC,
AB = AC ...[Given]
⇒ ∠C = ∠B ...(1) [Angles opposite to equal sides are equal]
Now, in ΔABC, ∠A = 90°
∠A + ∠B + ∠C = 180° ...[Angle sum property of Δ]
⇒ 90° + ∠B + ∠B = 180° ...[From (1)]
⇒ 2∠B = 90°
⇒ ∠B = 45°
⇒ ∠B = ∠C = 45° or ∠3 = ∠4 = 45°
Also, ∠1 = ∠2 = 45° ...[∵ AD is bisector of ∠A]
Also, ∠1 = ∠3, ∠2 = ∠4 = 45°
⇒ BD = AD, DC = AD ...(2) [Sides opposite to equal angles are equal]
Thus, BC = BD + DC = AD + AD ...[From (2)]
⇒ BC = 2AD
APPEARS IN
संबंधित प्रश्न
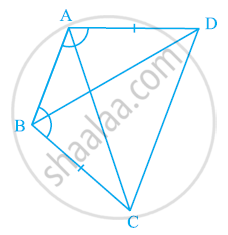
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
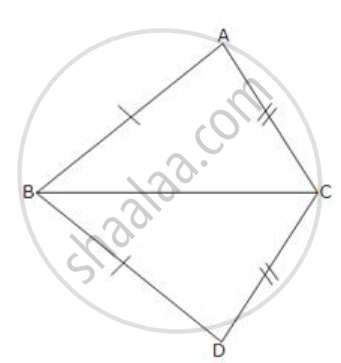
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

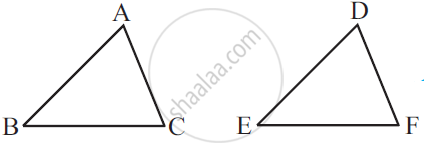
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
In the given figure, AB = DB and Ac = DC.
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
Which of the following is not a criterion for congruence of triangles?
