Advertisements
Advertisements
प्रश्न
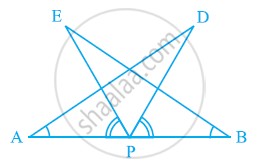
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
उत्तर
We have, P is the mid-point of AB.
∴ AP =BP
∠EPA = ∠DPB ...[Given]
Adding ∠EPD to both sides, we get:
∠EPA + ∠EPD = ∠DPB + ∠EPD
⇒ ∠APD = ∠BPE
i. Now, in △DAP and △EBP, we have
∠PAD = ∠PBE ...[∵ ∠BAD = ∠ABE]
AP = BP ...[Proved above]
∠DPA = ∠EPB ...[Proved above]
∴ △DAP ≌ △EBP ...[By ASA congruency]
ii. Since △DAP ≌ △EBP
⇒ AD = BE ...[By Corresponding Parts of Congruent Triangles]
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?

Explain, why ΔABC ≅ ΔFED.
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
Which of the following is not a criterion for congruence of triangles?
