Advertisements
Advertisements
प्रश्न
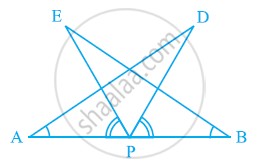
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
उत्तर
We have, P is the mid-point of AB.
∴ AP =BP
∠EPA = ∠DPB ...[Given]
Adding ∠EPD to both sides, we get:
∠EPA + ∠EPD = ∠DPB + ∠EPD
⇒ ∠APD = ∠BPE
i. Now, in △DAP and △EBP, we have
∠PAD = ∠PBE ...[∵ ∠BAD = ∠ABE]
AP = BP ...[Proved above]
∠DPA = ∠EPB ...[Proved above]
∴ △DAP ≌ △EBP ...[By ASA congruency]
ii. Since △DAP ≌ △EBP
⇒ AD = BE ...[By Corresponding Parts of Congruent Triangles]
APPEARS IN
संबंधित प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
