Advertisements
Advertisements
प्रश्न
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

उत्तर
In the given figure AB || FD,
⇒ ∠ABC =∠FDC
Also AC || GE,
⇒ ∠ACB = ∠GEB
Consider the two triangles ΔGBE and ΔFDC
∠B = ∠D ...(Corresponding angle)
∠C = ∠E ...(Corresponding angle)
Also given that
BD = CE
⇒ BD + DE = CE + DE
⇒ BE = DC
∴ By Angle-Side-Side-Angle criterion of congruence
ΔGBE ≅ ΔFDC
∴ `"GB"/"FD" = "BE"/"DC" = "GE"/"FC"`
But BE = DC
⇒ `"BE"/"DC" = "BE"/"BE"` = 1
∴ `"GB"/"FD" = "BE"/"DC"` = 1
⇒ GB = FD
∴ `"GE"/"FC" = "BE"/"DC"` = 1
⇒ GE = FC
APPEARS IN
संबंधित प्रश्न
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
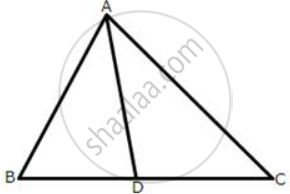
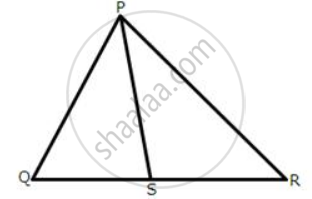
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
