Advertisements
Advertisements
प्रश्न
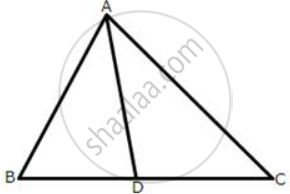
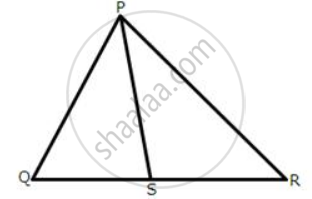
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
उत्तर
Given: AB = PQ ; BC = QR ; AD = PS
To prove: ΔABC ≅ ΔPQR
Proof:
BC = QR
2 BD = 2 QS
BD = QS ...(i)
In Δ ABD and Δ PQS
AB = PQ ...[Given]
BD = QS ...[From equation (i)]
AD = PS ...[Given]
∴ ΔABD ≅ ΔPQS ...[by SSS rule]
Then, ∠B = ∠Q ...[by CPCTC] ...(ii)
In ΔABC and ΔPQR
AB = PQ ...[Given]
∠B = ∠Q ...[ii]
BC = QR ...[Given]
∴ ΔABC ≅ ΔPQR ...[by SAS rule]
Hence proved.
APPEARS IN
संबंधित प्रश्न
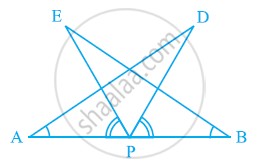
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
