Advertisements
Advertisements
प्रश्न
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
उत्तर
It is given that
∠B = 35°
∠C = 65°
AP is the bisector of ∠CAB
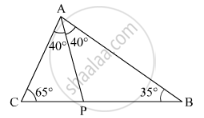
We have to arrangeAP, BPand CPin descending order.
In ΔACP we have
∠ACP = 65°
∠CAP = 40°(As AP is the bisector of ∠CAB
So AP > CP (Sides in front or greater angle will be greater) ........(1)
In ΔABP we have
∠BAP = 40°(As AP is the bisector of ∠CAB)
Since,
∠BAP >∠ABP
So BP > AP ..........(2)
Hence
From (1) & (2) we have
BP > AP > CP
APPEARS IN
संबंधित प्रश्न
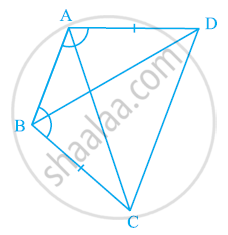
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

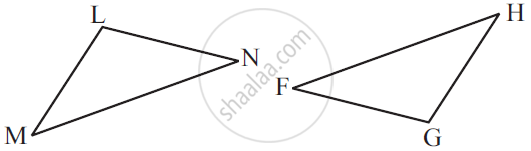
Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
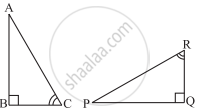
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
In the given figure, prove that:
CD + DA + AB + BC > 2AC

A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
