Advertisements
Advertisements
प्रश्न
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
उत्तर
Given: A(Δ ABC) is right-angled at B.
ABPQ and ACRS are squares
To Prove:
(i) ΔACQ ≅ ΔASB
(ii) CQ = BS
Proof:
(i)
∠ QAB = 90° ...[ ABPQ is a square ] ...(1)
∠ CAS = 90° ...[ ACRS is a square ] ...(2)
From (1) and (2) , We have
∠ QAB = ∠CAS ...(3)
Adding ∠BAC to both sides of (3), We have
∠ QAB + ∠BAC = ∠CAS+ ∠BAC
⇒ ∠QAC = ∠BAS ...(4)
In ΔACQ ≅ ΔASB, (by SAS)
QA = AB ...[ Sides of a square ABPQ ]
∠QAC = ∠SAB ...[ From(4) ]
AC = AS ...[ sides of a square ACRS ]
∴ By Side -Angle-Side criterion of congruence,
ΔACQ ≅ ΔASB
(ii)
The corresponding parts of the congruent triangles are congruent,
∴ CQ = SB ...[ c.p.c.t. ]
APPEARS IN
संबंधित प्रश्न
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
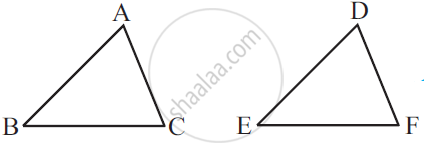
You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?

You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

Explain, why ΔABC ≅ ΔFED.
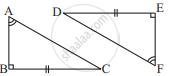
In the given figure, prove that:
CD + DA + AB > BC
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
