Advertisements
Advertisements
प्रश्न
In the given figure, prove that:
CD + DA + AB > BC
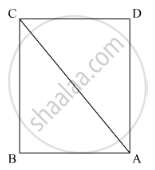
उत्तर
We have to prove that CD + DA + AB > BC
In ΔACD we have
CD + DA > CA (As sum of two sides of triangle is greater than third one)
⇒ CD + DA + AB > CA + AB (Adding AB both sides)
CD + DA + AB > BC Proved.
APPEARS IN
संबंधित प्रश्न
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
Use the information in the given figure to prove:
- AB = FE
- BD = CF

The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
