Advertisements
Advertisements
प्रश्न
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
उत्तर
Given: A ΔABQ in which AB is bisected at P
PQ is perpendicular to AB
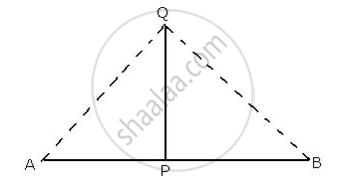
We need to prove that
QA = QB
Proof:
In ΔAPQ and ΔBPQ
AP = PB ...[ P is the mid-point of AB ]
∠QPA = ∠QPB = 90° ...[ PQ is perpendicular to AB ]
PQ = PQ ...[ Common]
∴ By Side-Angel-Side criterion of congruence,
ΔQAP ≅ ΔQBP
The corresponding parts of the congruent triangles are
congruent.
∴ QA = QB ...[ c.p.c.t ]
APPEARS IN
संबंधित प्रश्न
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

In the given figure, prove that:
CD + DA + AB + BC > 2AC

If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
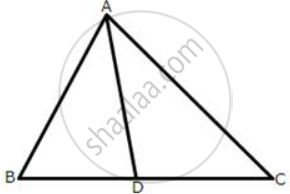
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

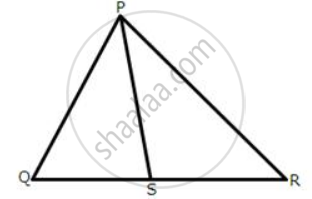
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
