Advertisements
Advertisements
प्रश्न
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
उत्तर
Given: ABC is an isosceles triangle with AB = AC and BD and CE are its two medians.
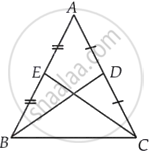
To prove: BD = CE
Proof: In triangle ABC,
AB = AC ...[Given]
`1/2 AB = 1/2 AC`
AE = AD ...[D is the mid-point of AC and E is the mid-point of AB]
Now, in triangle ABD and triangle ACE,
AB = AC ...[Given]
∠A = ∠A ...[Common angle]
AE = AD ...[Above proved]
Now, by SAS criterion of congruence, we get
ΔABD ≅ ΔACE
BD = CE ...[CPCT]
Hence proved.
APPEARS IN
संबंधित प्रश्न
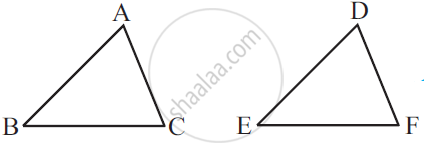
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?

Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
