Advertisements
Advertisements
Question
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
Solution
Given: ABC is an isosceles triangle with AB = AC and BD and CE are its two medians.
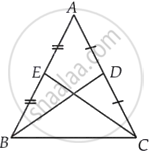
To prove: BD = CE
Proof: In triangle ABC,
AB = AC ...[Given]
`1/2 AB = 1/2 AC`
AE = AD ...[D is the mid-point of AC and E is the mid-point of AB]
Now, in triangle ABD and triangle ACE,
AB = AC ...[Given]
∠A = ∠A ...[Common angle]
AE = AD ...[Above proved]
Now, by SAS criterion of congruence, we get
ΔABD ≅ ΔACE
BD = CE ...[CPCT]
Hence proved.
APPEARS IN
RELATED QUESTIONS
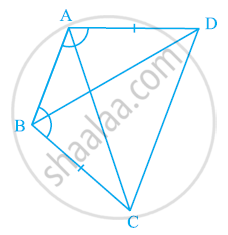
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

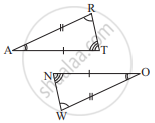
You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ΔRAT ≅ ?
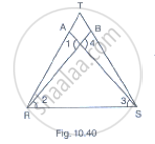
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
