Advertisements
Advertisements
प्रश्न
In the following diagram, ABCD is a square and APB is an equilateral triangle.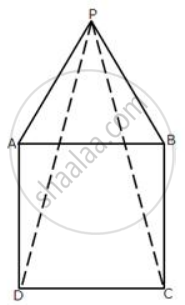
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
उत्तर
Given: ABCD is a Square and ΔAPB is an equilateral triangle.
(i) Proof: In ΔAPB,
AP = PB = AB ...[ APB is an equilateral triangle ]
Also, we have,
∠PBA = ∠PAB = ∠APB = 60° ...(1)
Since ABCD is a square, we have
∠A =∠ B = ∠C = ∠D = 90° ...(2)
Since ∠DAP = ∠A + ∠PAB ..(3)
⇒ ∠DAP = 90° + 60°
⇒ ∠DAP = 150° ...[ from (1) and (2) ] ...(4)
Similarly ∠CBP = ∠B + ∠PBA
⇒ ∠CBP = 90° + 60°
⇒ ∠CBP = 150° ...[ from (1) and (2) ] ...(5)
⇒ ∠DAP = ∠CBP ....[ from (1) and (2) ] ...(6)
In ΔAPD and ΔBPC
AD = BC ...[ Sides of square ABCD ]
∠DAP = ∠CBP ...[ from(6) ]
AP= BP [ Sides of equilateral ΔAPB ]
∴ By Side-AAngel-SIde Criterion of Congruence, we have,
ΔAPD ≅ ΔBPC
(ii)
AP = PB = AB ....[ ΔAPB is an equilateral triangle ] ...(7)
AB = BC = CD = DA ...[ Sides of square ABCD ] ...(8)
From (7) and (8), we have
AP = DA aand PB = BC ... (9)
In ΔAPD,
AP = DA ...[ from (9) ]
∠ADP = ∠APD ...[ Angel opposite to equal sides are equal ] ...(10)
∠ADP + ∠APD+ +∠DAP + 180° ...[ Sum of angel of a triangle = 180° ]
⇒ ∠ADP + ∠ADP + 150° = 180° [ from (3), ∠DAP =150° from (10), ∠ADP = ∠APD ]
⇒ ∠ADP + ∠ADP = 180° - 150°
⇒ 2∠ADP = 30°
⇒ ∠ADP = `30^circ/2`
⇒∠ADP= 15°
We have ∠PDC =∠D - ∠ADP
⇒∠PDC =90° - 15°
⇒∠PDC =75° ...(11)
In ΔBPC,
PB = BC ...[ from (9) ]
∴ ∠PCB =∠ BPC ...[Angel opposite to equal sides are equal ] ... (12)
∠PCB + ∠BPC + ∠CBP = 180° ....[ Sum of angel of a triangle = 180° ]
⇒ ∠PCB + ∠PCB + 30° = 180° ....[ from (5), ∠CBP = 150° from (12) , ∠PCB =∠BPC ]
⇒ 2∠PCB = 180° - 150°
⇒ 2∠PCB = `30^circ/2`
⇒ ∠PCB = 15°
We have ∠PCD = ∠C - ∠PCB
⇒ ∠PCD = 90° - 15°
⇒ ∠PCD = 75° ... (13)
In ΔDPC,
∠PDC = 75°
∠PCD = 75°
∠PCD + ∠PDC + ∠DPC = 180° ...[ Sum of angles of a triangle = 180° ]
⇒ 75° + 75° + ∠DPC = 180°
⇒ ∠DPC = 180° - 150°
⇒ ∠DPC = 30°
∴ Angles of DPC, are: 75°, 30° , 75°
APPEARS IN
संबंधित प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.
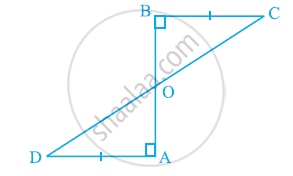
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
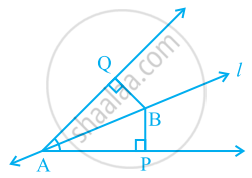
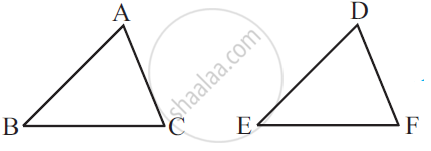
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =
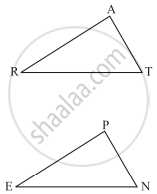
You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?

In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 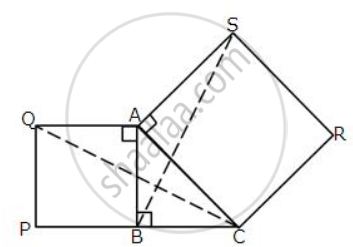
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.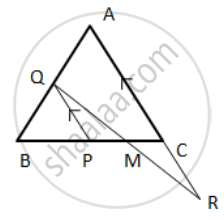
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
