Advertisements
Advertisements
प्रश्न
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
उत्तर
ΔABC is an equilateral triangle,
So, each of its angles equals 60°.
QP is parallel to AC,
⇒ ∠PQB = ∠RAQ = 60°
ln ΔQBP,
∠PQB = ∠BQP = 60°
So, ∠PBQ + ∠BQP + ∠BPQ = 180° ....(angle sum property)
⇒ 60°+ 60° + ∠BPQ = 180°
⇒ ∠BPQ = 60°
So, ΔBPQ is an equilateral triangle.
⇒ QP = BP
⇒ QP = CR ....(i)
Now, ∠QPM + ∠BPQ = 180° ...(linear pair)
⇒ ∠QPM+ 60°= 180°
⇒ ∠QPM = 120°
Also, ∠RCM+ ∠ACB = 180° ...(linear pair)
⇒ ∠RCM+ 60° = 180°
⇒ ∠RCM = 120°
ln ΔRCM and ΔQMP,
∠RCM = ∠QPM ....(each is 120°)
∠RMC = ∠QMP ...(vertically opposite angles)
QP= CR ....(from(i))
⇒ ΔRCM ≅ ΔQMP ....(AAS congruence criterion)
So, CM = PM
⇒ QR bisects PC.
APPEARS IN
संबंधित प्रश्न
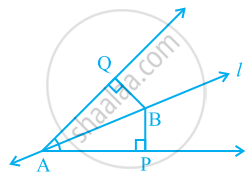
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
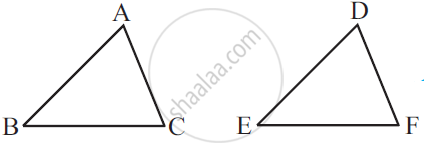
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
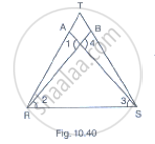
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
In the given figure, prove that:
CD + DA + AB + BC > 2AC

In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
