Advertisements
Advertisements
प्रश्न
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
उत्तर

Given: In quadrilateral ABCD, AD = BC and BD = AC.
To Prove:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
Proof:
In ΔABD and ΔBAC,
AD = BC ....(given)
BD = CA ....(given)
AB = AB ....(common)
∴ ΔABD ≅ ΔBAC ....(by SSS congruence criterion)
`{:(∠"ADB" = ∠"BCA"), (∠"DAB" = ∠"CBA"):}} ...("c.p.c.t.")`
APPEARS IN
संबंधित प्रश्न
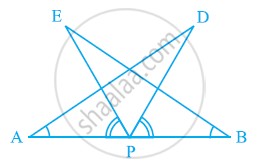
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

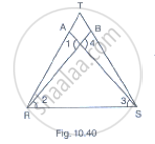
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
