Advertisements
Advertisements
प्रश्न
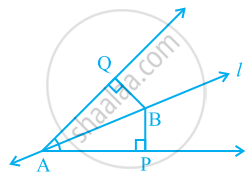
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
उत्तर
We have, l is the bisector of ∠QAP.
∴ ∠QAB = ∠PAB
and ∠Q = ∠P ...[Each 90°]
⇒ ∠ABQ = ∠ABP ...[By angle sum property of △]
i. Now, in △APB and △AQB, we have
∠ABP = ∠ABQ ...[Proved above]
AB = BA ...[Common]
∠PAB ≅ ∠QAB ...[Given]
△APB ≅ △AQB ...[By ASA congruency]
ii. Since, △APB ≅ △AQB
⇒ BP = BQ ...[By Corresponding parts of congruent triangles]
i.e., [Perpendicular distance of B from AP] = [Perpendicular distance of B from AQ]
Thus, the point B is equidistant from the arms of ∠A.
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
