Advertisements
Advertisements
प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

उत्तर
Given: In quadrilateral ABCD, AC = AD and AB bisects ∠A.
To prove: △ABC ≌ △ABD
Proof: In △ABC and △ABD,
AC = AD ...[Given]
∠BAC = ∠BAD ...[∵ AB bisects ∠A]
AB = AB ...[Common]
∴ △ABC ≌ △ABD ...[By SAS congruence rule]
Hence, BC = BD ...[Corresponding parts of congruent triangles]
APPEARS IN
संबंधित प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

Explain, why ΔABC ≅ ΔFED.
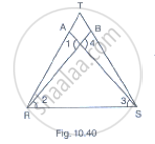
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
In the given figure, AB = DB and Ac = DC.
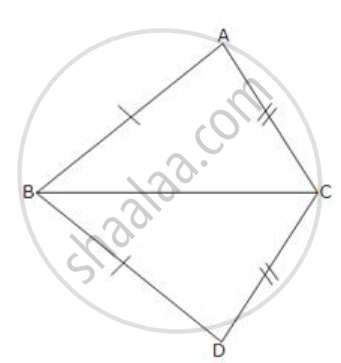
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
