Advertisements
Advertisements
प्रश्न
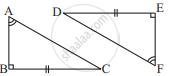
Explain, why ΔABC ≅ ΔFED.
उत्तर
Given that, ∠ABC = ∠FED (1)
∠BAC = ∠EFD (2)
The two angles of ΔABC are equal to the two respective angles of ΔFED. Also, the sum of all interior angles of a triangle is 180º. Therefore, third angle of both triangles will also be equal in measure.
∠BCA = ∠EDF (3)
Also, given that, BC = ED (4)
By using equation (1), (3), and (4), we obtain
ΔABC ≅ ΔFED (ASA criterion)
APPEARS IN
संबंधित प्रश्न
You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
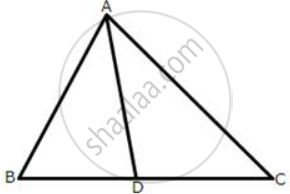
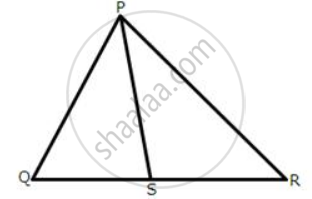
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
