Advertisements
Advertisements
Question
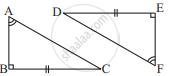
Explain, why ΔABC ≅ ΔFED.
Solution
Given that, ∠ABC = ∠FED (1)
∠BAC = ∠EFD (2)
The two angles of ΔABC are equal to the two respective angles of ΔFED. Also, the sum of all interior angles of a triangle is 180º. Therefore, third angle of both triangles will also be equal in measure.
∠BCA = ∠EDF (3)
Also, given that, BC = ED (4)
By using equation (1), (3), and (4), we obtain
ΔABC ≅ ΔFED (ASA criterion)
APPEARS IN
RELATED QUESTIONS
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?

If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
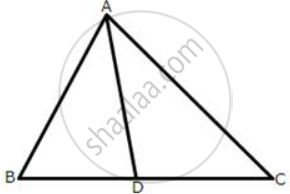
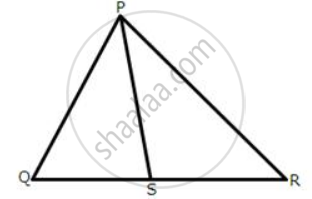
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
