Advertisements
Advertisements
Question
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

Solution
l || m ...[Given]
AC is a transversal.
So, ∠DAC = ∠ACB ...[Alternate angles]
p || q ...[Given]
AC is a transversal.
So, ∠BAC = ∠ACD ...[Alternate angles]
Now, △ABC and △CDA,
∠ACB = ∠DAC ...[Proved above]
∠BAC = ∠ACD ...[Proved above]
AC = AC ...[Common]
△ABC ≌ △CDA ...[By AAS congruence rule]
APPEARS IN
RELATED QUESTIONS
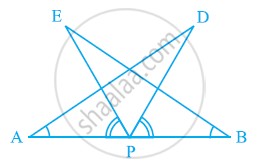
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
