Advertisements
Advertisements
प्रश्न
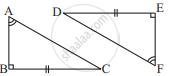
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

उत्तर
l || m ...[Given]
AC is a transversal.
So, ∠DAC = ∠ACB ...[Alternate angles]
p || q ...[Given]
AC is a transversal.
So, ∠BAC = ∠ACD ...[Alternate angles]
Now, △ABC and △CDA,
∠ACB = ∠DAC ...[Proved above]
∠BAC = ∠ACD ...[Proved above]
AC = AC ...[Common]
△ABC ≌ △CDA ...[By AAS congruence rule]
APPEARS IN
संबंधित प्रश्न
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

Explain, why ΔABC ≅ ΔFED.
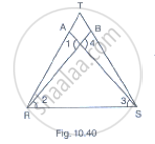
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
In the given figure, AB = DB and Ac = DC.
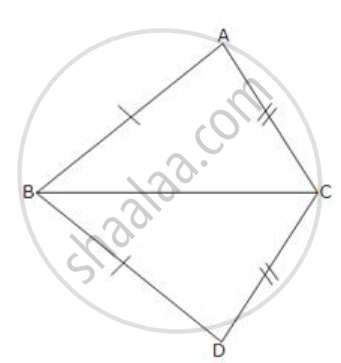
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that: BD = CD

