Advertisements
Advertisements
Question
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
Solution
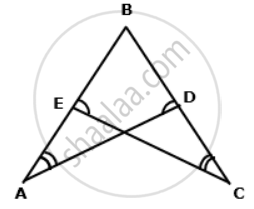
In triangles AOE and COD,
∠A = ∠C ...(given)
∠AOE = ∠COD ...(vertically opposite angles)
∴ ∠A + ∠AOE = ∠C + ∠COD
⇒ 180° - ∠AEO = 180° - ∠CDO
⇒ ∠AEO = ∠ CDO ….(i)
Now, ∠AEO + ∠OEB = 180° ....(linear pair)
And, ∠CDO + ∠ODB = 180° ....(linear pair)
∴ ∠AEO + ∠OEB = ∠CDO + ∠ODB
⇒ ∠OEB = ∠ODB ....[ Using (i) ]
⇒ ∠CEB = ∠ADB ….(ii)
Now, in ΔABD and ΔCBE,
∠A = ∠C ....(given)
∠ADB = ∠CEB ...[ From (ii) ]
AB = BC ....(given)
⇒ ΔABD ≅ ΔCBE ....(by AAS congruence criterion).
APPEARS IN
RELATED QUESTIONS
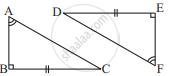
Explain, why ΔABC ≅ ΔFED.
ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that: BD = CD

In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
