Advertisements
Advertisements
Question
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
Solution
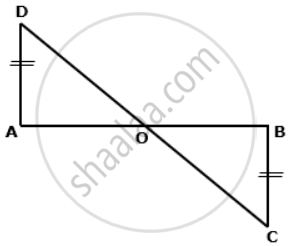
In ΔAOD and ΔBOC,
∠ AOD = ∠ BOC ....(vertically opposite angles)
∠ DAO = ∠ CBO ....(each 90°)
AD = BC ....(given)
∴ ΔAOD ≅ ΔBOC ...(by AAS congruence criterion)
⇒ AO = BO ...(c.p.c.t.)
⇒ O is the mid-point of AB.
Hence, CD bisects AB.
APPEARS IN
RELATED QUESTIONS
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
