Advertisements
Advertisements
Question
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

Options
52°
76°
156°
104°
Solution
We are given that;
ΔABC , is isosceles
AB = AC
∠B = ∠C
∠C = 52
And AB || CD
We are asked to find angle x
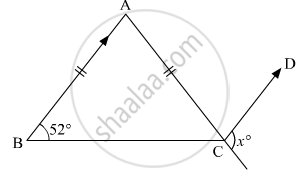
From the figure we have
∠ACB = 52°
Therefore,
∠A = `180° - 2 xx 52° `
= 76°
Since AB || DC , so
∠ACD = ∠BAC
= 76°
Now
x + 76 = 180
= 180 - 76
= 104
APPEARS IN
RELATED QUESTIONS
You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
Use the information in the given figure to prove:
- AB = FE
- BD = CF

The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
