Advertisements
Advertisements
प्रश्न
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
उत्तर
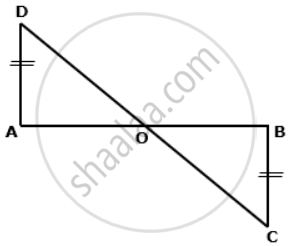
In ΔAOD and ΔBOC,
∠ AOD = ∠ BOC ....(vertically opposite angles)
∠ DAO = ∠ CBO ....(each 90°)
AD = BC ....(given)
∴ ΔAOD ≅ ΔBOC ...(by AAS congruence criterion)
⇒ AO = BO ...(c.p.c.t.)
⇒ O is the mid-point of AB.
Hence, CD bisects AB.
APPEARS IN
संबंधित प्रश्न
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
