Advertisements
Advertisements
प्रश्न
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
उत्तर
Given: in the figure, O is center of the circle, and AB is chord. P is a point on AB such that AP = PB.
We need to prove that, OP ⊥ AB
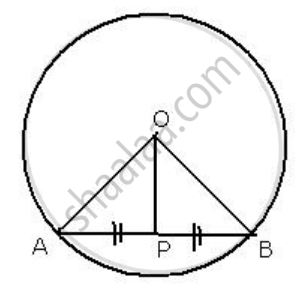
Construction: Join OA and OB
Proof:
In ΔOAP and ΔOBP
OA = OB ...[radii of the same circle]
OP = OP ...[common]
AP = PB ...[given]
∴ By Side-Side-Side criterion of congruency,
ΔOAP ≅ ΔOBP
The corresponding parts of the congruent triangles are congruent.
∴ ∠OPA = ∠OPB ...[by c.p.c.t]
But ∠OPA + ∠OPB = 180° ...[linear pair]
∴ ∠OPA = ∠OPB = 90°
Hence OP ⊥ AB.
APPEARS IN
संबंधित प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In the given figure, prove that:
CD + DA + AB > BC
Use the information in the given figure to prove:
- AB = FE
- BD = CF

In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
