Advertisements
Advertisements
प्रश्न
In ∆ABC, AB = AC. Show that the altitude AD is median also.
उत्तर
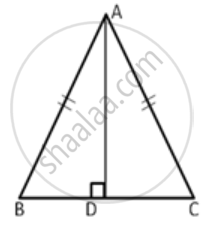
In ∆ABD and ∆ADC,
AB = AC ...(Since is an isosceles triangle)
AD = AD ...(common side)
∠ADB = ∠ADC ...(Since AD is the altitude so each is 90°)
⇒ ΔADB ≅ ΔADC ...(RHS congruence criterion)
BD = DC ...(cpct)
⇒ AD is the median.
APPEARS IN
संबंधित प्रश्न
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
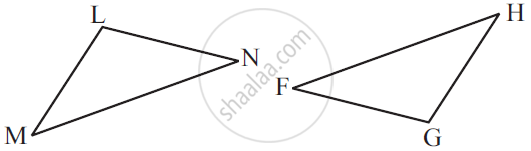
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
In the given figure, prove that:
CD + DA + AB + BC > 2AC

If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
