Advertisements
Advertisements
प्रश्न
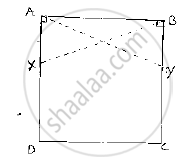
ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
उत्तर
Given that ABCD is a square, X and Y are points on sides AD and BC respectively such that AY = BX.
We have to prove BY = AX and ∠BAY = ∠ABX
Join B and X, A and Y.
Since, ABCD is a square ⇒ ∠ DAB = ∠CBA =90°
⇒ ∠XAB= ∠YBA=90° .............(1)
Now, consider triangle XAB and YBA
We have
∠XAB=∠YBA=90° ...........[From (1)]
BX=AY [given]
And AB=BA [Common side]
So, by RHS congruence criterion, we have ΔXAB≅ΔYBA
Now, we know that corresponding parts of congruent triangles are equal.
∴ BY=AX and ∠BAY=∠ABX
∴ Hence proved
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
