Advertisements
Advertisements
Question
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
Solution
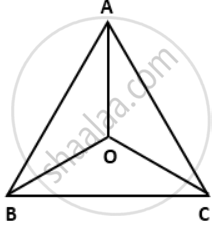
In ΔABC,
AB = AC
⇒ ∠B = ∠C ...( angles opposite to equal sides are equal )
⇒ `1/2 ∠"B" = 1/2∠"C"`
⇒ ∠OBC = ∠OCB ...[ ∵ OB and OC are bisectors of ∠B and ∠C respectively, ∠OBC = `1/2∠"B" and ∠"OCB" = 1/2∠"C"` ] ...(i)
⇒ OB = OC ...( Sides opposite to equal angles are equal ) ...(ii)
Now, in ΔABO and ΔACO,
AB = AC ...( given )
∠OBC = ∠OCB ...[ from(i) ]
OB = OC ...[ from(ii) ] ...( proved )
∴ ΔABO ≅ ΔACO ...( by SAS congruence criterion )
⇒ ∠BAO = ∠CAO ...( c.p.c.t. )
⇒ AO bisects ∠BAC ...(proved)
APPEARS IN
RELATED QUESTIONS
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

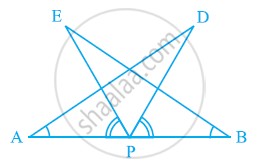
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
