Advertisements
Advertisements
Question
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
Solution
It is given that
ΔABC ≅ ΔDEF
AB = DE
BC = EF
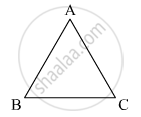
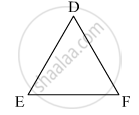
Since, the triangles ABC and DEF are congruent, therefore,
∠A = ∠D
∠B = ∠E
∠C = ∠F
APPEARS IN
RELATED QUESTIONS
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
