Advertisements
Advertisements
प्रश्न
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
उत्तर
It is given that
ΔABC ≅ ΔDEF
AB = DE
BC = EF
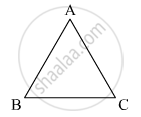
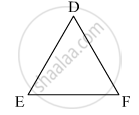
Since, the triangles ABC and DEF are congruent, therefore,
∠A = ∠D
∠B = ∠E
∠C = ∠F
APPEARS IN
संबंधित प्रश्न
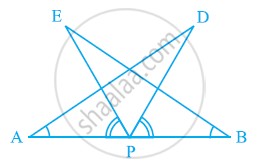
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
