Advertisements
Advertisements
प्रश्न
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
उत्तर
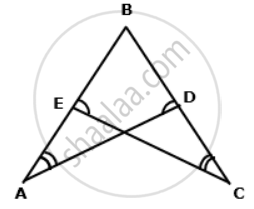
In triangles AOE and COD,
∠A = ∠C ...(given)
∠AOE = ∠COD ...(vertically opposite angles)
∴ ∠A + ∠AOE = ∠C + ∠COD
⇒ 180° - ∠AEO = 180° - ∠CDO
⇒ ∠AEO = ∠ CDO ….(i)
Now, ∠AEO + ∠OEB = 180° ....(linear pair)
And, ∠CDO + ∠ODB = 180° ....(linear pair)
∴ ∠AEO + ∠OEB = ∠CDO + ∠ODB
⇒ ∠OEB = ∠ODB ....[ Using (i) ]
⇒ ∠CEB = ∠ADB ….(ii)
Now, in ΔABD and ΔCBE,
∠A = ∠C ....(given)
∠ADB = ∠CEB ...[ From (ii) ]
AB = BC ....(given)
⇒ ΔABD ≅ ΔCBE ....(by AAS congruence criterion).
APPEARS IN
संबंधित प्रश्न
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
In the given figure, prove that:
CD + DA + AB > BC
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
