Advertisements
Advertisements
प्रश्न
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
उत्तर
ABCD is a parallelogram in which ∠A and ∠C are obtuse.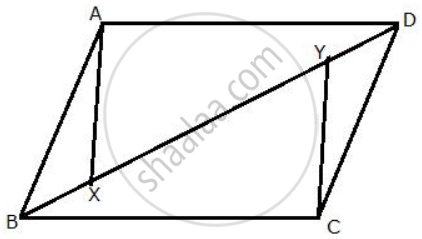
Points X and Y are taken on the diagonal BD.
Such that ∠XAD = ∠YCB = 90°.
We need to prove that XA = YC
Proof:
ln ΔXAD and ΔYCB
∠XAD = ∠YCB= 90° ...[ Given ]
AD = BC ...[ Opposite sides of a parallelogram ]
∠ADX = ∠CBY ...[ Alternate angles ]
∴ By Angle-Side-Angle criterion of congruence,
ΔXAD ≅ ΔYCB
The corresponding parts of the congruent triangles are congruent.
∴ XA = YC ...[ c.p.c.t. ]
Hence proved.
APPEARS IN
संबंधित प्रश्न
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
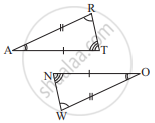
In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ΔRAT ≅ ?
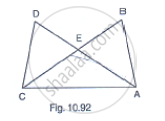
In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
