Advertisements
Advertisements
Question
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
Solution
In the triangle ABC it is given that
AB = AC, BE and CFare medians.
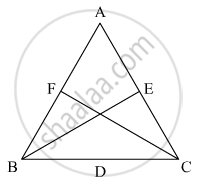
We have to show that BE CF
To show BF = CF we will show that ΔBFC ≅ ΔBEC
In triangle ΔBFC and ΔBEC
As AB = AC, so
∠FBC = ∠ECF .........(1)
BC=BC (common sides) ........(2)
Since,
AB = AC
`1/2 AB =1/2 AC `
As F and E are mid points of sides AB and AC respectively, so
BF = CE ..........(3)
From equation (1), (2), and (3)
ΔBFC and ΔBEC
Hence FC = BE Proved.
APPEARS IN
RELATED QUESTIONS
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

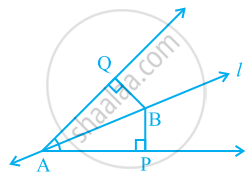
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Prove that the perimeter of a triangle is greater than the sum of its altitudes.
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
