Advertisements
Advertisements
Question
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
Solution
Given: In the figure, O is the center of the circle, and AB is a chord. P is a point on AB such that AP=PB.
We need to prove that, AAP=BP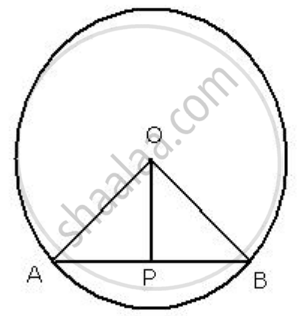
Construction: Join OA and OB
Proof:
In right triangles ΔOAP and ΔOBP
Hypotenuse OA=OB .....[ radii of the same circle ]
Side OP= OP ...[ common ]
∴ By Right Angle- Hypotenuse- Side criterion of congruency, ΔOAP ≅ ΔOBP
The corresponding parts of the congruent triangles are congruent.
∴ AP=BP .....[ by c.p.c.t ]
Hence proved.
APPEARS IN
RELATED QUESTIONS
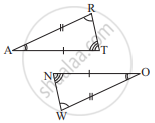
In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ΔRAT ≅ ?
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
Use the information in the given figure to prove:
- AB = FE
- BD = CF

In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
