Advertisements
Advertisements
Question
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
Solution
In Δ ABC and Δ DEF,
AB = DE ...[ Given ]
∠B = ∠E ...[ Given ]
BC = EF ...[ Given ]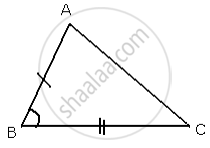
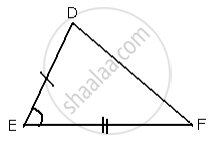
By Side - Angle - Side criterion of congruency, the triangles
Δ ABC and Δ DEF are congruent to each other.
∴ Δ ABC ≅ Δ DEF
APPEARS IN
RELATED QUESTIONS
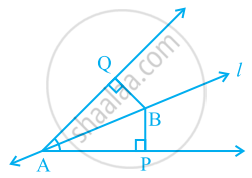
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
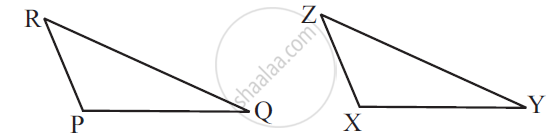
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
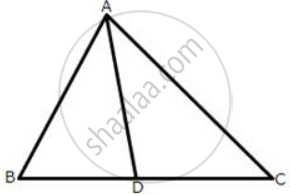
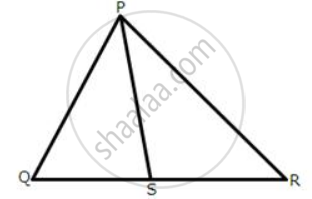
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
In the following diagram, AP and BQ are equal and parallel to each other. 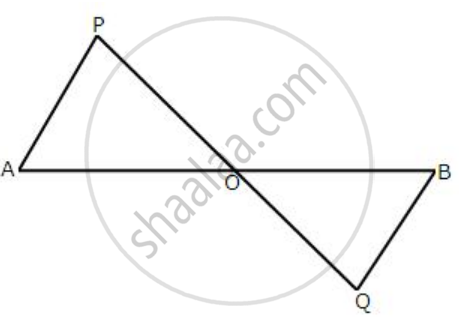
Prove that: AB and PQ bisect each other.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
