Advertisements
Advertisements
Question
In the given figure, prove that:
CD + DA + AB + BC > 2AC

Solution
We have to prove that CD + DA + AB + BC > 2AC
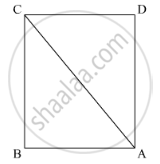
In ΔABC we have
AB + BC > AC (As sum of two sides of triangle is greater than third one) ........(1)
In ΔACDwe have
AD + CD > AC (As sum of two sides of triangle is greater than third one) .........(2)
Hence
Adding (1) & (2) we get AB + BC + AC + CD > 2AC Proved.
APPEARS IN
RELATED QUESTIONS
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

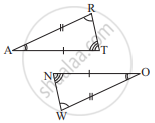
In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ΔRAT ≅ ?
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
