Advertisements
Advertisements
प्रश्न
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
उत्तर
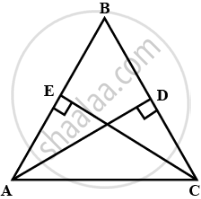
ln ΔABD and ΔCBE,
AB = BC ....(given)
AD ⊥ BC
CE ⊥ AB
To proved:
In ΔABD & ΔCBE
∠ ADB = ∠ CEB = 90° ....[Perpendiculars]
∠B = ∠B ....(Common angle)
AB = BC
∴ ΔABD ≅ ΔCBE ....(by AAS congruence)
⇒ AD = CE ...(c.p.c.t.c)
APPEARS IN
संबंधित प्रश्न
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
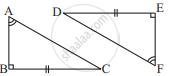
Explain, why ΔABC ≅ ΔFED.
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
