Advertisements
Advertisements
Question
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.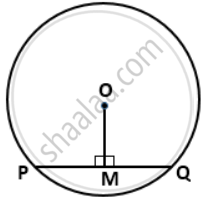
Solution
Given:
In the figure, O is centre of the circle and PQ is a chord.
OM ⊥ PQ
To prove: PM = QM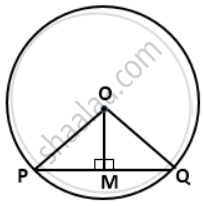
Construction: Join Op and OQ
Proof:
In right triangles ΔOPM and ΔOQM,
OP = OQ ....[radii of the same circle]
OM = OM ....[common]
∴ By right angle-Hypotenuse-Side criterion of congruency,
ΔOPM ≅ΔOQM
The corresponding parts of the congruent triangles are congruent.
∴ PM = QM.
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
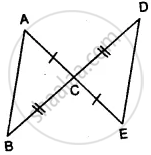
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.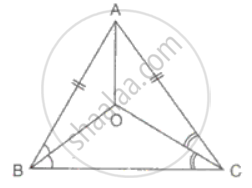
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.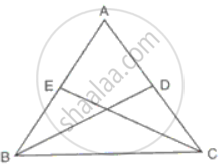
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.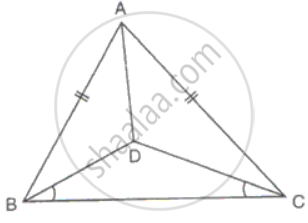
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent angles
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles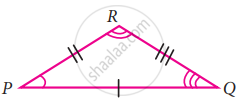
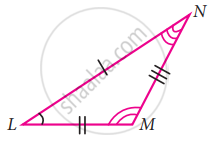
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆XYZ ≅ ∆MLN
