Advertisements
Advertisements
Question
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.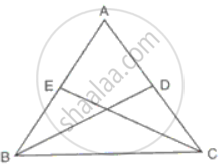
Solution
CE is median to AB
⇒ AE = BE ......(i)
BD is median to AC
⇒ AD = DC ......(i)
But AB =AC ......(iii)
Therefore from (i), (ii) and (iii)
BE = CD
In ΔBEC and ΔBDC
BE = CD
∠EBC = ∠DCB ...(angles opposites to equal sides are equal)
BC = BC ...(common)
Therefore, ΔBEC ≅ ΔBDC ...(SAS criteria)
Hence, BD = CE.
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(EF)`
In a squared sheet, draw two triangles of equal areas such that
The triangles are congruent.
What can you say about their perimeters?
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
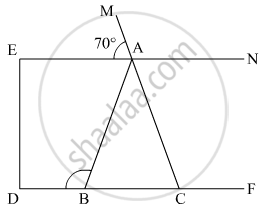
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
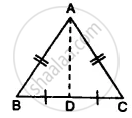
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
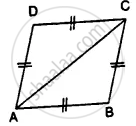
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
