Advertisements
Advertisements
Question
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Options
True
False
Solution
This statement is False.
Explanation:
Since side of one triangle must be equal to its corresponding side of another triangle.
APPEARS IN
RELATED QUESTIONS
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true:
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.
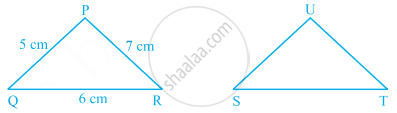
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆ABC ≅ ∆LMN
