Advertisements
Advertisements
Question
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
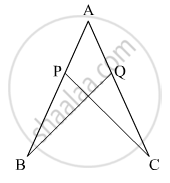
Solution
It is given that
AB = AC , and ∠B = ∠C
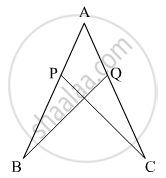
We have to prove that BQ = CP
We basically will prove ΔABQ ≅ ΔACP to show BQ = CP
In ΔABQ and ΔACP
∠B = ∠C (Given)
AB = AC(Given)
And ∠A is common in both the triangles
So all the properties of congruence are satisfied
So ΔABQ ≅ ΔACP
Hence BQ = CP Proved.
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
In a squared sheet, draw two triangles of equal areas such that
The triangles are congruent.
What can you say about their perimeters?
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.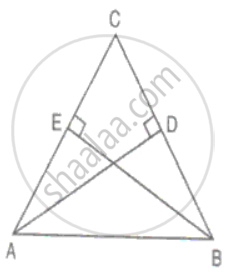
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
The congruent figures super impose each other completely.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆ABC ≅ ∆LMN
