Advertisements
Advertisements
Question
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
Options
100°
120°
110°
130°
Solution
Let ABCbe isosceles triangle
Then
AB = AC
∠B = ∠C
Now it is given that vertex angle is 2 times the sum of base angles
⇒∠A = 2 ∠(B+ C)
⇒∠A = 2 ∠(∠B + ∠B ) (As ∠B = ∠C)
⇒∠A = 2 (2∠B)
⇒∠A = 4 ∠B
Now
∠A + ∠B + ∠C = 180° (Property of triangle)
4∠B + ∠B + ∠B = 180° (Since ∠A = 4∠B, and ∠B = ∠C )
6∠B = 180°
∠B = 30°
∠A = 4∠B
`= 4 xx 30°`
= 120°
APPEARS IN
RELATED QUESTIONS
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

By ______ test
ΔXYZ ≅ ΔLMN
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
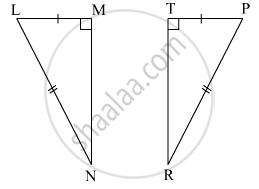
By ______ test
ΔLMN ≅ ΔPTR
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 5cm,BC = 7cm,CA = 9cm);
ΔKLM;(KL = 7cm,LM = 5cm,KM = 9cm).
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
