Advertisements
Advertisements
Question
In a ΔABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
Options
20°
40°
60°
80°
Solution
In the triangle ABC it is given that
AB = AC
∠ACD = 100°
We have to find ∠A
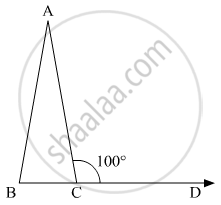
Now ∠ACD + ∠ACB = 180° (linear pair)
SinceAB = AC
So, ∠B = ∠C (by isosceles triangle)
This implies that
∠B =∠C
= 180° - 100
= 80
Now,
∠A + ∠B + ∠C = 180° (Property of triangle)
∠A + 80° + 80° = 180°
∠A = 180° - 160°
∠A = 20°
APPEARS IN
RELATED QUESTIONS
Mark the correct alternative in each of the following:
If ABC ≅ ΔLKM, then side of ΔLKM equal to side AC of ΔABC is
If ΔABC ≅ ΔABC is isosceles with
Which of the following is not a criterion for congruence of triangles?
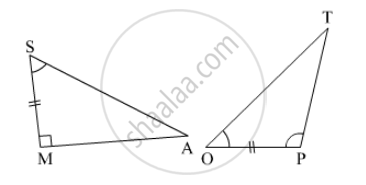
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
State, whether the pairs of triangles given in the following figures are congruent or not:
In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.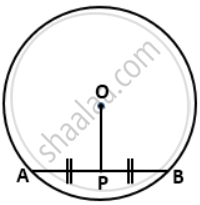
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
Two right-angled triangles ABC and ADC have the same base AC. If BC = DC, prove that AC bisects ∠BCD.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆ABC ≅ ∆LMN
