Advertisements
Advertisements
Question
In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.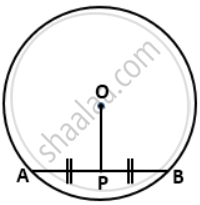
Solution
Given:
In the figure, O is centre of the circle and ab is chord.
P is the mid-point of AB ⇒ AP = PB
To prove: OP ⊥ AB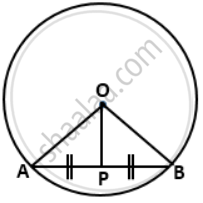
Construction: Join OA and OB
Proof:
In ΔOAP and ΔOBP
OA = OB ....[radii of the same circle]
OP = OP ....[common]
AP = PB ....[given]
∴ By Side-Side-Side criterion of congruency,
ΔOAP ≅ ΔOBP
The corresponding parts of the congruent triangles are congruent.
∴ ∠OPA = ∠OPB
But ∠OPA + ∠OPB = 180° ....[linear pair]
∴ ∠OPA = ∠OPB = 90°
Hence OP ⊥ AB.
APPEARS IN
RELATED QUESTIONS
If ΔPQR≅ ΔEFD, then ∠E =
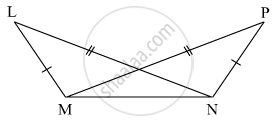
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
State, whether the pairs of triangles given in the following figures are congruent or not:

In the given figure, prove that: ∆ ABD ≅ ∆ ACD
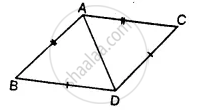
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
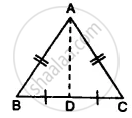
In ΔABC and ΔPQR and, AB = PQ, BC = QR and CB and RQ are extended to X and Y respectively and ∠ABX = ∠PQY. = Prove that ΔABC ≅ ΔPQR.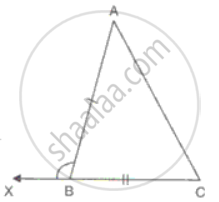
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
Which of the following rule is not sufficient to verify the congruency of two triangles
If AB = QR, BC = PR and CA = PQ, then ______.
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side BC of ∆ABC so that the two triangles are congruent? Give reason for your answer.
