Advertisements
Advertisements
Question
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
Solution
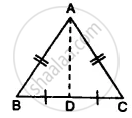
Given: In the figure,
AB = AC
BD = CD
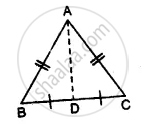
To prove:
- Δ ABD ≅ Δ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
Proof: In Δ ABD and Δ ACD
AD = AD ...(common)
AB = AC ...(given)
BD = CD ...(given)
(i) ∴ Δ ABD ≅ Δ ACD ...(SSS axiom)
(ii) ∴ ∠B = ∠C ...(c.p.c.t.)
(iii) ∠ADB = ∠ADC ...(c.p.c.t.)
But ∠ADB + ∠ADC = 180° ...(Linear pair)
∴ ∠ADB = ∠ADC
(iv) ∠ADB = ∠ADC
= `(180°)/2`
= 90°
APPEARS IN
RELATED QUESTIONS
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
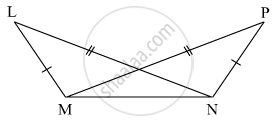
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
In the following figure, OA = OC and AB = BC.

Prove that: AD = CD
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) AM = AN (ii) ΔAMC ≅ ΔANB

State, whether the pairs of triangles given in the following figures are congruent or not:

In the figure, ∠CPD = ∠BPD and AD is the bisector of ∠BAC. Prove that ΔCAP ≅ ΔBAP and CP = BP.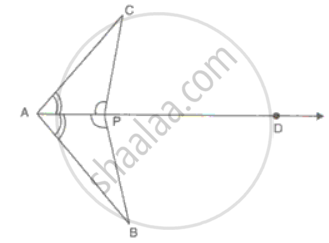
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆STU ≅ ∆DEF
