Advertisements
Advertisements
Question
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
Options
BC = EF
AC = DE
AC = EF
BC = DE
Solution
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if AC = DE.
Explanation:
Given, in ΔABC and ΔDEF,
AB = DF and ∠A = ∠D
We know that, two triangles will be congruent by ASA rule, if two angles and the included side of one triangle are equal to the two angles and the included side of other triangle.
∴ AC = DE
APPEARS IN
RELATED QUESTIONS
ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true:
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
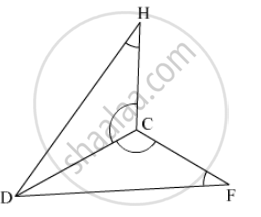
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 5cm,BC = 7cm,CA = 9cm);
ΔKLM;(KL = 7cm,LM = 5cm,KM = 9cm).
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.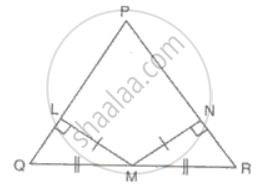
In the figure, RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.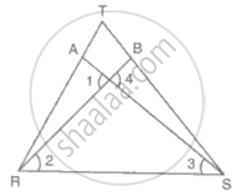
In ΔABC, X and Y are two points on AB and AC such that AX = AY. If AB = AC, prove that CX = BY.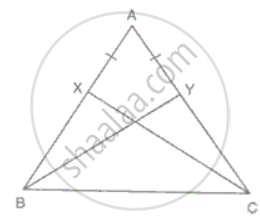
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.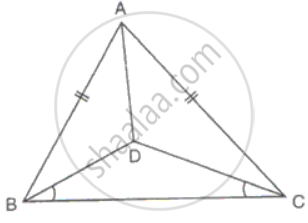
Two figures are congruent, if they have the same shape.
